これは井口和基博士のホームページです。
Octet Truss Spirals |
|---|
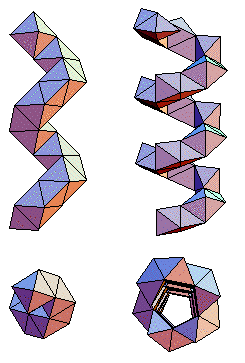
These are octet
truss spirals with a four- or five- fold symmetry axis.
They mimic the α-helices of proteins found long ago by Linus Pauling
who got the Nobel prize for this discovery. The concept of octet
truss
was first found by Buckminster Fuller who found the famous Fullerene
(soccer ball molecule) structure known as the geodesic dome. As
I have
shown in the octet truss spirals, the very concept of the octet
truss
also dominates the three-dimensional protein structures as well.
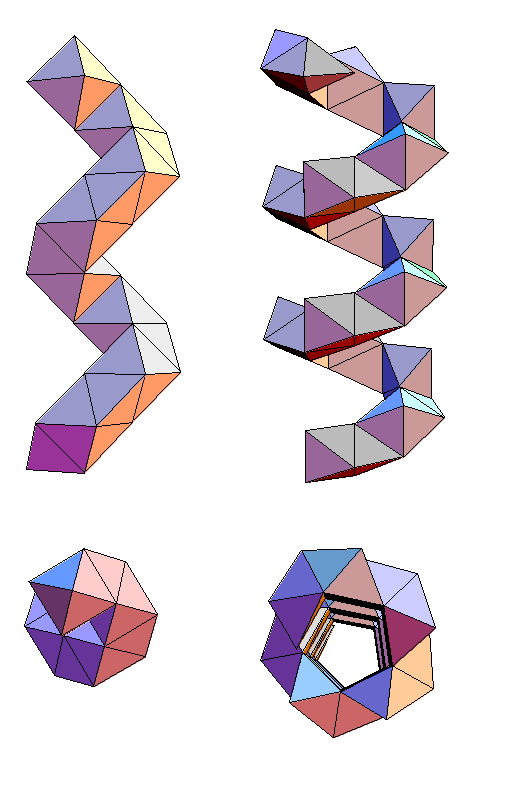
Octet Truss Spirals or Helices
図の作り方(How to generate the figure)
The Mathematica
program is as follows:
You just substitute it into the window and run the program.
If you want to change view angle, you may adapt to change
ViewPoint->{-0.810, -3.340, -0.150}
to any set of the values.
Enjoy it! (11 Nov 2K2)
-------------------------------------
(* Octet spirals with four-fold axial symmetry *)
Helix:=
Table[{
{
Polygon[{{0,0,4*n+1},{1,0,4*n},{0,1,4*n}}],
Polygon[{{0,0,4*n+1},{0,1,4*n},{-1,0,4*n}}],
Polygon[{{0,0,4*n+1},{-1,0,4*n},{0,-1,4*n}}],
Polygon[{{0,0,4*n+1},{0,-1,4*n},{1,0,4*n}}],
Polygon[{{1,0,4*n},{0,-1,4*n},{0,0,4*n-1}}],
Polygon[{{1,0,4*n},{0,0,4*n-1},{0,1,4*n}}],
Polygon[{{0,0,4*n-1},{0,-1,4*n},{-1,0,4*n}}],
Polygon[{{0,1,4*n},{0,0,4*n-1},{-1,0,4*n}}]
},
{
Polygon[{{1,0,4*n+2},{2,0,4*n+1},{1,1,4*n+1}}],
Polygon[{{1,0,4*n+2},{1,1,4*n+1},{0,0,4*n+1}}],
Polygon[{{1,0,4*n+2},{0,0,4*n+1},{1,-1,4*n+1}}],
Polygon[{{1,0,4*n+2},{1,-1,4*n+1},{2,0,4*n+1}}],
Polygon[{{2,0,4*n+1},{1,-1,4*n+1},{1,0,4*n}}],
Polygon[{{2,0,4*n+1},{1,0,4*n},{1,1,4*n+1}}],
Polygon[{{1,0,4*n},{1,-1,4*n+1},{0,0,4*n+1}}],
Polygon[{{1,1,4*n+1},{1,0,4*n},{0,0,4*n+1}}]
},
{
Polygon[{{1,1,4*n+3},{2,1,4*n+2},{1,2,4*n+2}}],
Polygon[{{1,1,4*n+3},{1,2,4*n+2},{0,1,4*n+2}}],
Polygon[{{1,1,4*n+3},{0,1,4*n+2},{1,0,4*n+2}}],
Polygon[{{1,1,4*n+3},{1,0,4*n+2},{2,1,4*n+2}}],
Polygon[{{2,1,4*n+2},{1,0,4*n+2},{1,1,4*n+1}}],
Polygon[{{2,1,4*n+2},{1,1,4*n+1},{1,2,4*n+2}}],
Polygon[{{1,1,4*n+1},{1,0,4*n+2},{0,1,4*n+2}}],
Polygon[{{1,2,4*n+2},{1,1,4*n+1},{0,1,4*n+2}}]
},
{
Polygon[{{0,1,4*n+4},{1,1,4*n+3},{0,2,4*n+3}}],
Polygon[{{0,1,4*n+4},{0,2,4*n+3},{-1,1,4*n+3}}],
Polygon[{{0,1,4*n+4},{-1,1,4*n+3},{0,0,4*n+3}}],
Polygon[{{0,1,4*n+4},{0,0,4*n+3},{1,1,4*n+3}}],
Polygon[{{1,1,4*n+3},{0,0,4*n+3},{0,1,4*n+2}}],
Polygon[{{1,1,4*n+3},{0,1,4*n+2},{0,2,4*n+3}}],
Polygon[{{0,1,4*n+2},{0,0,4*n+3},{-1,1,4*n+3}}],
Polygon[{{0,2,4*n+3},{0,1,4*n+2},{-1,1,4*n+3}}]
},
{
Polygon[{{0,0,4*n+1},{1,0,4*n},{0,-1,4*n}}],
Polygon[{{0,0,4*n+1},{1,0,4*n},{1,-1,4*n+1}}],
Polygon[{{1,-1,4*n+1},{1,0,4*n},{0,-1,4*n}}],
Polygon[{{0,0,4*n+1},{1,-1,4*n+1},{0,-1,4*n}}]
},
{
Polygon[{{0,1,4*n},{-1,1,4*n-1},{0,0,4*n-1}}],
Polygon[{{0,1,4*n},{-1,1,4*n-1},{-1,0,4*n}}],
Polygon[{{-1,0,4*n},{-1,1,4*n-1},{0,0,4*n-1}}],
Polygon[{{0,1,4*n},{-1,0,4*n},{0,0,4*n-1}}]
},
{
Polygon[{{1,1,4*n+3},{1,2,4*n+2},{0,1,4*n+2}}],
Polygon[{{0,2,4*n+3},{1,2,4*n+2},{0,1,4*n+2}}],
Polygon[{{0,2,4*n+3},{1,1,4*n+3},{1,2,4*n+2}}],
Polygon[{{0,2,4*n+3},{1,1,4*n+3},{0,1,4*n+2}}]
},
{
Polygon[{{1,0,4*n+2},{2,1,4*n+2},{1,0,4*n}}],
Polygon[{{1,0,4*n+2},{2,1,4*n+2},{2,0,4*n+1}}],
Polygon[{{2,0,4*n+1},{2,1,4*n+2},{1,0,4*n}}],
Polygon[{{1,0,4*n+2},{2,0,4*n+1},{1,0,4*n}}]
}
},
{n, 0,1}
]
Show[Graphics3D[Helix],ViewPoint->{-0.810, -3.340, -0.150},
Boxed->False]
(* Octet spirals with five-fold axial symmetry *)
a:=Sqrt[3]/2;
b:=3/4;
phi:=2*Pi/5;
Helix5:=
Table[{
{
Polygon[{{a*Cos[phi*n],a*Sin[phi*n],n/2},
{a*Cos[phi*(n+1)],a*Sin[phi*(n+1)],1/2+n/2},
{a*Cos[phi*(n+1)],a*Sin[phi*(n+1)],-1/2+n/2}}],
Polygon[{{a*Cos[phi*n],a*Sin[phi*n],n/2},
{2*b*Cos[phi*(2*n+1)/2],2*b*Sin[phi*(2*n+1)/2],1/2+n/2},
{2*b*Cos[phi*(2*n+1)/2],2*b*Sin[phi*(2*n+1)/2],-1/2+n/2}}],
Polygon[{{a*Cos[phi*n],a*Sin[phi*n],n/2},
{a*Cos[phi*(n+1)],a*Sin[phi*(n+1)],-1/2+n/2},
{2*b*Cos[phi*(2*n+1)/2],2*b*Sin[phi*(2*n+1)/2],-1/2+n/2}}],
Polygon[{{a*Cos[phi*n],a*Sin[phi*n],n/2},
{a*Cos[phi*(n+1)],a*Sin[phi*(n+1)],1/2+n/2},
{2*b*Cos[phi*(2*n+1)/2],2*b*Sin[phi*(2*n+1)/2],1/2+n/2}}],
Polygon[{{a*Cos[phi*(n+1)],a*Sin[phi*(n+1)],1/2+n/2},
{a*Cos[phi*(n+1)],a*Sin[phi*(n+1)],-1/2+n/2},
{2*a*Cos[phi*(n+1)],2*a*Sin[phi*(n+1)],n/2}}],
Polygon[{{a*Cos[phi*(n+1)],a*Sin[phi*(n+1)],1/2+n/2},
{2*b*Cos[phi*(2*n+1)/2],2*b*Sin[phi*(2*n+1)/2],1/2+n/2},
{2*a*Cos[phi*(n+1)],2*a*Sin[phi*(n+1)],n/2}}],
Polygon[{{a*Cos[phi*(n+1)],a*Sin[phi*(n+1)],-1/2+n/2},
{2*b*Cos[phi*(2*n+1)/2],2*b*Sin[phi*(2*n+1)/2],-1/2+n/2},
{2*a*Cos[phi*(n+1)],2*a*Sin[phi*(n+1)],n/2}}],
Polygon[{{2*a*Cos[phi*(n+1)],2*a*Sin[phi*(n+1)],n/2},
{2*b*Cos[phi*(2*n+1)/2],2*b*Sin[phi*(2*n+1)/2],1/2+n/2},
{2*b*Cos[phi*(2*n+1)/2],2*b*Sin[phi*(2*n+1)/2],-1/2+n/2}}]
},
{
Polygon[{{a*Cos[phi*(n+1)],a*Sin[phi*(n+1)],1/2+n/2},
{a*Cos[phi*(n+1)],a*Sin[phi*(n+1)],-1/2+n/2},
{2*a*Cos[phi*(n+1)],2*a*Sin[phi*(n+1)],n/2}}],
Polygon[{{a*Cos[phi*(n+1)],a*Sin[phi*(n+1)],1/2+n/2},
{a*Cos[phi*(n+1)],a*Sin[phi*(n+1)],-1/2+n/2},
{2*b*Cos[phi*(2*n+3)/2],2*b*Sin[phi*(2*n+3)/2],n/2}}],
Polygon[{{a*Cos[phi*(n+1)],a*Sin[phi*(n+1)],1/2+n/2},
{2*a*Cos[phi*(n+1)],2*a*Sin[phi*(n+1)],n/2},
{2*b*Cos[phi*(2*n+3)/2],2*b*Sin[phi*(2*n+3)/2],n/2}}],
Polygon[{{a*Cos[phi*(n+1)],a*Sin[phi*(n+1)],-1/2+n/2},
{2*a*Cos[phi*(n+1)],2*a*Sin[phi*(n+1)],n/2},
{2*b*Cos[phi*(2*n+3)/2],2*b*Sin[phi*(2*n+3)/2],n/2}}]
},
{
Polygon[{{a*Cos[phi*(n+1)],a*Sin[phi*(n+1)],1/2+n/2},
{a*Cos[phi*(n+1)],a*Sin[phi*(n+1)],-1/2+n/2},
{2*b*Cos[phi*(2*n+3)/2],2*b*Sin[phi*(2*n+3)/2],n/2}}],
Polygon[{{2*b*Cos[phi*(2*n+3)/2],2*b*Sin[phi*(2*n+3)/2],n/2},
{a*Cos[phi*(n+2)],a*Sin[phi*(n+2)],n/2},
{a*Cos[phi*(n+1)],a*Sin[phi*(n+1)],-1/2+n/2}}],
Polygon[{{2*b*Cos[phi*(2*n+3)/2],2*b*Sin[phi*(2*n+3)/2],n/2},
{a*Cos[phi*(n+2)],a*Sin[phi*(n+2)],n/2},
{a*Cos[phi*(n+1)],a*Sin[phi*(n+1)],1/2+n/2}}],
Polygon[{{a*Cos[phi*(n+2)],a*Sin[phi*(n+2)],n/2},
{a*Cos[phi*(n+1)],a*Sin[phi*(n+1)],1/2+n/2},
{a*Cos[phi*(n+1)],a*Sin[phi*(n+1)],-1/2+n/2}}]
}
},
{n,1,15}
];
Show[Graphics3D[Helix5],ViewPoint->{-0.060, -0.060, 1.900},
Boxed->False]